An actual golden ellipsoid not of revolution
09/03/2024

This is a real (i.e. not AI generated) photo of an actual object. It is the very first prototype of an ellipsoid in the general case. It is a creation made by numerunique. Note that an ellipsoid "of revolution" is more common as it can easily by done with a lathe.

Yes, it is a wooden crafted object made with a CNC milling machine. So why golden? Because its proportion respects two golden ratios: one between the largest dimension with respect to the intermediary dimension, another between the intermediary dimension and the smallest - see below.

Manufacturing this tiny object was sort of a challenge.

Usually, numerunique uses a CAD software, the best professional one, to create an object. Starting with a sketch composed with common shapes easy to use and adapt, a 3D representation is simple to obtain. Then, picking in predefined common toolpath strategies, the G-code is automatically produced after its execution has been beautifully simulated to spot any potential hazards that could end in adverse events up to damaging the CNC milling machine. All this is very convenient.

However, there is no way of modelling an ellipsoid not of revolution with this CAD software; the usual process abort at its beginning.

This is probably why such a real photo of an actual object representing an ellipsoid (not of revolution) cannot be found on the web. Its easier in the case of an ellipsoid of revolution and even more easier with the specific case of ellipsoid: a sphere. Every one has played whith marbles, haven't they?

Ellipsoids are a type of quadratic surface with a beautiful canonical equation: $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$.

By the way, for the case illustrated by the picture above, the golden ratios are $a=fb$ and $b=fc$ where $f=\frac{1+\sqrt{5}}{2}$.

Anyway, you can easily deduce from the equation of an ellipsoid that its intersection with any horizontal plan between the altitudes $-c$ and $c$ is… an ellipse! This induce a simple strategy to mill an ellipsoid but leads to another rather straightforward problem with apparently no published solution: how to compute a polygon tangent to an ellipse? Solving this problem raises another question: how to compute the distance between a point and an ellipse?

Once these problems solved by a double nested dichotomy, numerunique had to develop a crude tool to check the validity of the underlying computations necessary to mill an ellipsoid.

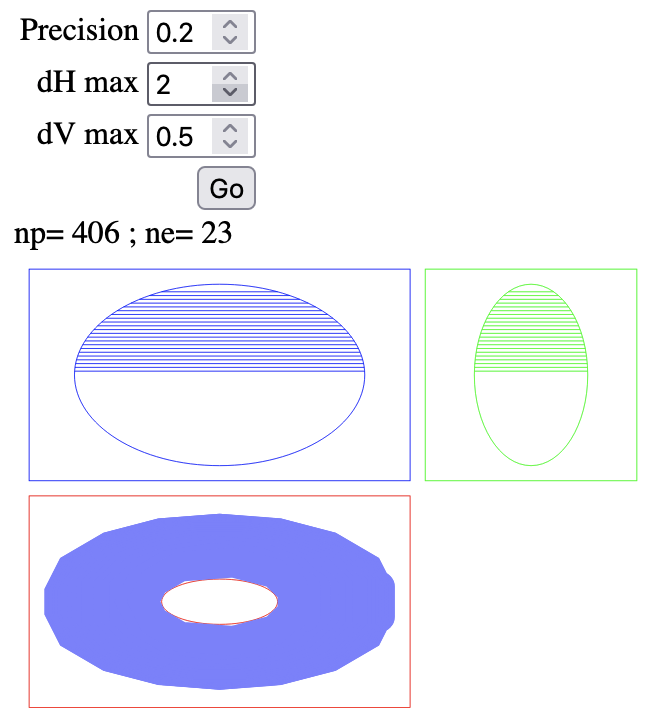
Then numerunique had to develop a program to convert it to G-code…

Moreover, to prevent the risk of damaging its CNC milling machine, numerunique also had to develop a simulation of the execution of this G-code.

As usual the first execution of the actual milling, although successful, revealed a lot of improvements remaining to make.

Précédent | Suivant