A new ellipsoides' property!
13/05/2024

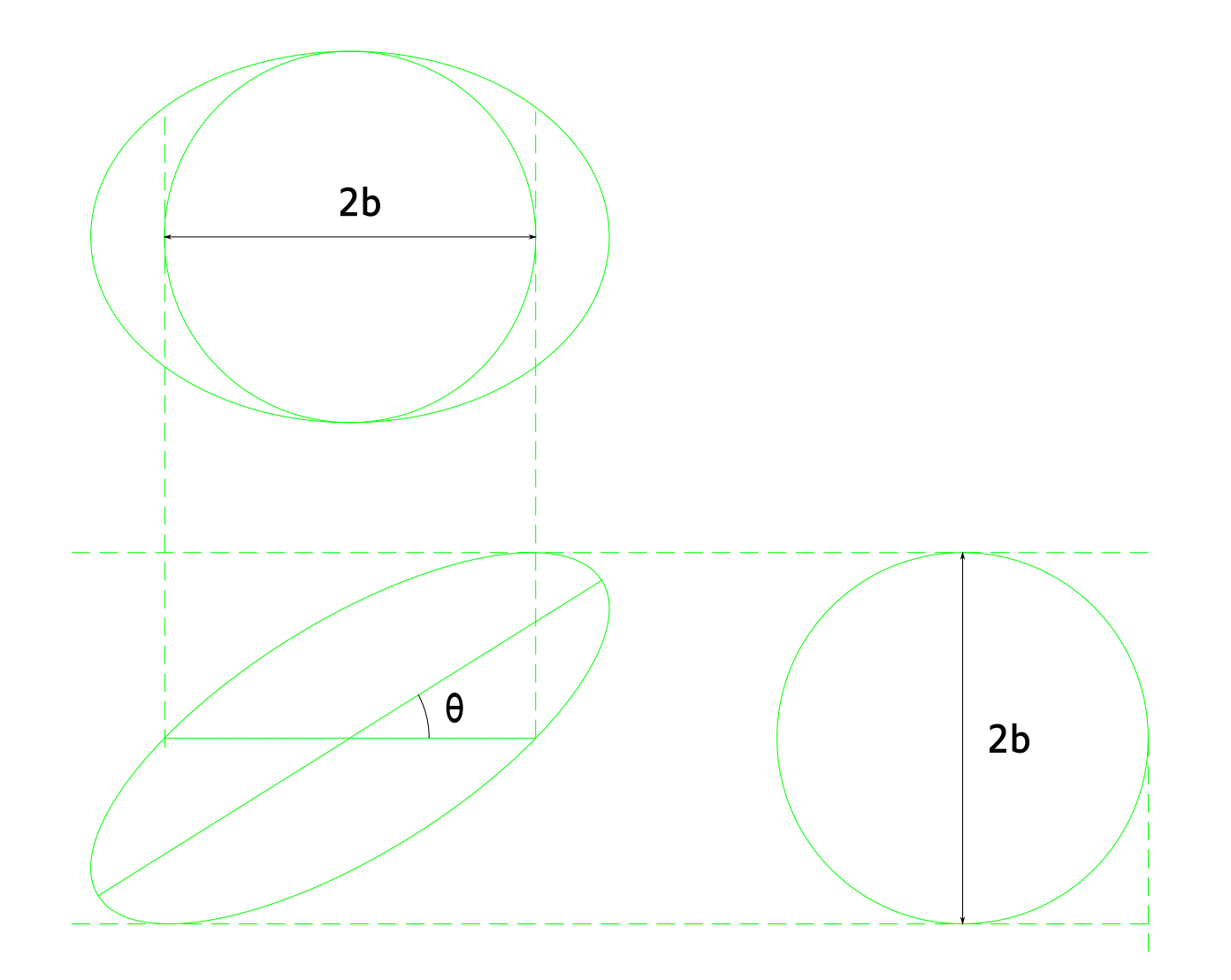
Ellipsoids have an interesting well known property: when tilted at a well chosen angle, its non void intersections with an horizontal plan are circles.

Hence the unavoidable idea to build a support that illustrate this property.

Observation

Checking the computation made to build this support, it appeared that the projection of the ellipsoid thus tilted to a vertical plan looks like a disk!

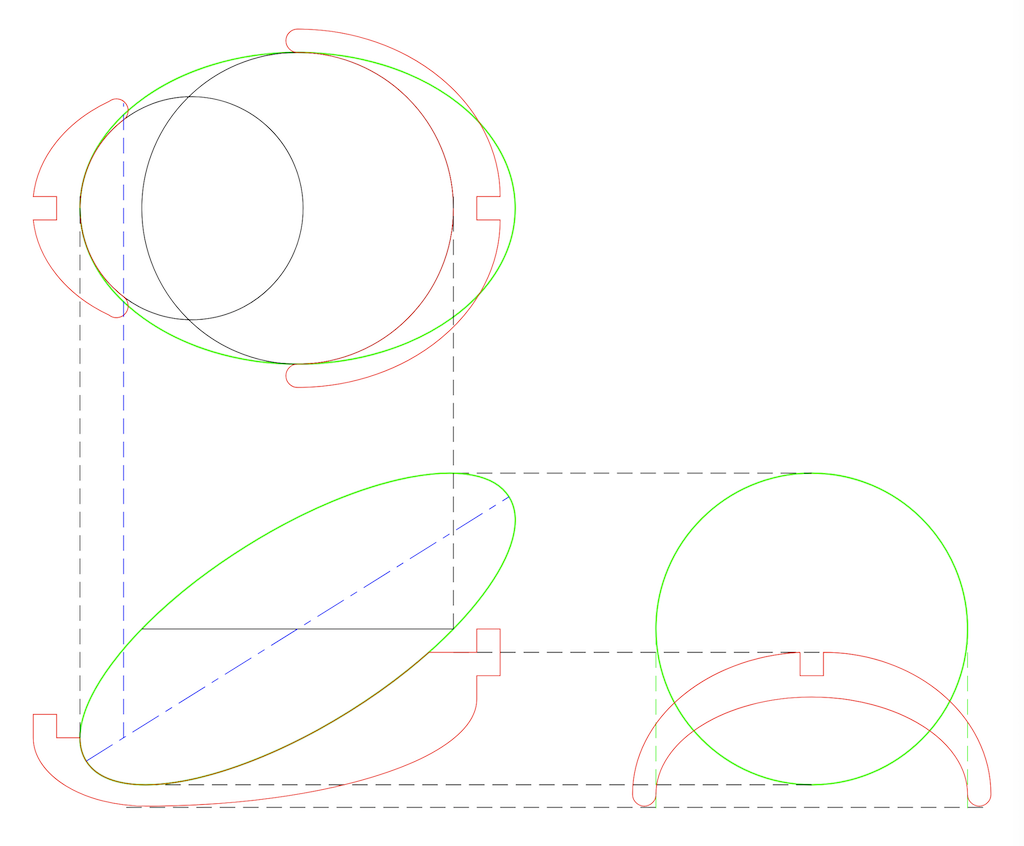
This is somehow confirmed by the shadow of the actual object on its intended support.

The existence of an angle at which the shadow of an ellipsoid is a disk is quite obvious. The coincidence of that angle with the one that gives circular horizontal intersection is a surprise. This does not happen to all ellipsoids. There should be the same proportion between its length and width than its width an height.

Formally expressed, the question is rather simple. Given the canonical equation of an ellipsoid $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ with $a=kb$ and $b=kc$ and θ the angle at which the ellipsoid is tilted such as its intersection with the plan Oxy is a circle, is its projection on the plan Oyz also a disk of radius b?

Formal proof

The formal proof of this property was given by Jean-François Burnol as follows.

The ellipsoid equation tilted to the proper angle θ becomes:

$\frac{{(\cos \theta x+\sin \theta z)}^2}{k^2{b}^2}+\frac{y^2}{b^2}+k^2\frac{{(\cos \theta z-\sin \theta x)}^2}{b^2}=1$

Having circles for $z=0$ yields:

$\frac{{\cos }^2\theta }{k^2}+k^2{\sin }^2\theta =1$

Thus:

${\sin }^2\theta ={(k^2+1)}^{-1}$

${\cos }^2\theta =k^2{(k^2+1)}^{-1}$

$\sin \theta \cos \theta =k{(k^2+1)}^{-1}$

For the latest eqation we choose the positive solution.

Thus:

$x^2+2\sin \theta \cos \theta xz(\frac{1}{k^2}-k^2)+z^2(\frac{{\sin }^2\theta }{k^2}+k^2{\cos }^2\theta )+y^2\le b^2$

And:

$x^2+2(\frac{1}{k}-k)xz+y^2+z^2\frac{1+k^6}{k^2(k^2+1)}-b^2\le 0$

For the projection of the ellipsoid on the Oyz plane the reduced discriminant of this second degree trinomial in x must verify:

${(\frac{1}{k}-k)}^2{z}^2-y^2-z^2\frac{1+k^6}{k^2(k^2+1)}+b^2\ge 0$

And as:

${(\frac{1}{k}-k)}^2-\frac{1+k^6}{k^2(k^2+1)}=-1$

We have:

$x^2+z^2\le b^2$

Which is indeed the inequality of a disk of radius b.

Précédent | Suivant